A ball of mass $10 \mathrm{~kg}$ moving with a velocity $10 \sqrt{3} \mathrm{~m} / \mathrm{s}$ along the $\mathrm{x}$-axis, hits another ball of mass $20 \mathrm{~kg}$ which is at rest. After the collision, first ball comes to rest while the second ball disintegrates into two equal pieces. One piece starts moving along $y$-axis with a speed of $10 \mathrm{~m} / \mathrm{s}$. The second piece starts moving at an angle of $30^{\circ}$ with respect to the $x$-axis. The velocity of the ball moving at $30^{\circ}$ with $\mathrm{x}$-axis is $\mathrm{xm} / \mathrm{s}$. The configuration of pieces after collision is shown in the figure below. The value of $x$ to the nearest integer is
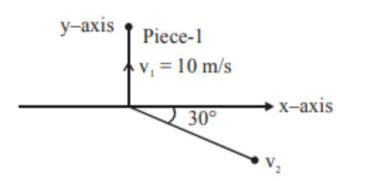
Let velocity of $2^{\text {nd }}$ fragment is $\vec{v}$ then by
conservation of linear momentum
$10(10 \sqrt{3}) \hat{\mathrm{i}}=(10)(10 \hat{\mathrm{j}})+10 \overrightarrow{\mathrm{v}}$
$\Rightarrow \vec{v}=10 \sqrt{3} \hat{i}-10 \hat{j}$
$|\overrightarrow{\mathrm{v}}|=\sqrt{300+100}=\sqrt{400}=20 \mathrm{~m} / \mathrm{s}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
