Question.
A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. Give the magnitude and direction of the acceleration of the body.
A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. Give the magnitude and direction of the acceleration of the body.
solution:
$2 \mathrm{~m} / \mathrm{s}^{2}$, at an angle of $37^{\circ}$ with a force of $8 \mathrm{~N}$
Mass of the body, $m=5 \mathrm{~kg}$
The given situation can be represented as follows:
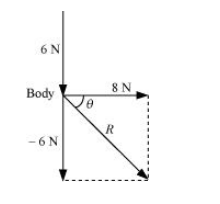
The resultant of two forces is given as:
$R=\sqrt{(8)^{2}+(-6)^{2}}=\sqrt{64+36}=10 \mathrm{~N}$
$\theta$ is the angle made by $R$ with the force of $8 \mathrm{~N}$
$\therefore \theta=\tan ^{-1}\left(\frac{-6}{8}\right)=-36.87^{\circ}$
The negative sign indicates that $\theta$ is in the clockwise direction with respect to the force of magnitude $8 \mathrm{~N}$.
As per Newton’s second law of motion, the acceleration (a) of the body is given as:
F = ma
$\therefore a=\frac{F}{m}=\frac{10}{5}=2 \mathrm{~m} / \mathrm{s}^{2}$
$2 \mathrm{~m} / \mathrm{s}^{2}$, at an angle of $37^{\circ}$ with a force of $8 \mathrm{~N}$
Mass of the body, $m=5 \mathrm{~kg}$
The given situation can be represented as follows:
The resultant of two forces is given as:
$R=\sqrt{(8)^{2}+(-6)^{2}}=\sqrt{64+36}=10 \mathrm{~N}$
$\theta$ is the angle made by $R$ with the force of $8 \mathrm{~N}$
$\therefore \theta=\tan ^{-1}\left(\frac{-6}{8}\right)=-36.87^{\circ}$
The negative sign indicates that $\theta$ is in the clockwise direction with respect to the force of magnitude $8 \mathrm{~N}$.
As per Newton’s second law of motion, the acceleration (a) of the body is given as:
F = ma
$\therefore a=\frac{F}{m}=\frac{10}{5}=2 \mathrm{~m} / \mathrm{s}^{2}$