A chord of length 30 cm is drawn at a distance of 8 cm from the centre of a circle.

Let AB be the chord of the given circle with centre O. The perpendicular distance from the centre of the circle to the chord is 8 cm.
Join OB.
Then OM = 8 cm and AB = 30 cm

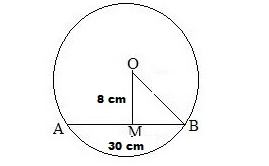
We know that the perpendicular from the centre of a circle to a chord bisects the chord.

$\therefore M B=\left(\frac{A B}{2}\right)=\left(\frac{30}{2}\right) \mathrm{cm}=15 \mathrm{~cm}$

From the right ΔOMB, we have:
OB2 = OM2 + MB2
⇒ OB2 = 82 + 152
⇒ OB2 = 64 + 225
⇒ OB2 = 289

$\Rightarrow O B=\sqrt{289} \mathrm{~cm}=17 \mathrm{~cm}$

Hence, the  required length of the radius is 17 cm.