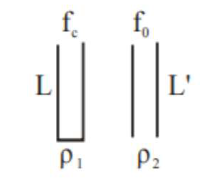
A closed organ pipe of length $\mathrm{L}$ and an open organ pipe contain gases of densities $\rho_{1}$ and $\rho_{2}$ respectively. The compressibility of gases are equal in both the pipes. Both the pipes are vibrating in their first overtone with same frequency. The length of the open pipe is_____ $\frac{x}{3} \mathrm{~L} \sqrt{\frac{\overline{\rho_{1}}}{\rho_{2}}}$ where $x$ is (Round off to the Nearest Integer)
(4)
$\mathrm{f}_{\mathrm{c}}=\mathrm{f}_{0}$
$\frac{3 \mathrm{~V}_{\mathrm{C}}}{4 \mathrm{~L}}=\frac{2 \mathrm{~V}_{0}}{2 \mathrm{~L}^{\prime}}$
$\frac{3 \mathrm{~V}_{\mathrm{C}}}{4 \mathrm{~L}}=\frac{\mathrm{V}_{0}}{\mathrm{~L}^{\prime}}$
$\mathrm{L}^{\prime}=\frac{4 \mathrm{~L}}{3} \frac{\mathrm{V}_{0}}{\mathrm{~V}_{\mathrm{C}}}=\frac{4 \mathrm{~L}}{3} \sqrt{\frac{\mathrm{B} \cdot \rho_{1}}{\rho_{2} \cdot \mathrm{B}}}$ (B is bulk modulus)
$=\frac{4 \mathrm{~L}}{3} \sqrt{\frac{\rho_{1}}{\rho_{2}}}$
$x=4$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
