A coaxial cable consists of an inner wire of radius 'a' surrounded by an outer shell of inner and outer radii ' $b$ ' and 'c' respectively. The inner wire carries an electric current $\mathrm{i}_{0}$, which is distributed uniformly across cross-sectional area. The outer shell carries an equal current in opposite direction and distributed uniformly. What will be the ratio of the magnetic field at a distance $x$ from the axis when (i) $\mathrm{x}<\mathrm{a}$ and (ii) $\mathrm{a}<\mathrm{x}<\mathrm{b}$ ?
Correct Option: 1
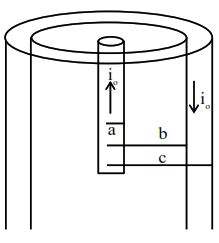
when $x $\mathrm{B}_{1}(2 \pi \mathrm{x})=\mu_{\mathrm{o}}\left(\frac{\mathrm{i}_{\mathrm{o}}}{\pi \mathrm{a}^{2}}\right) \pi \mathrm{x}^{2}$ $\mathrm{B}(2 \pi x)=\frac{\mu_{0} i_{0} x^{2}}{a^{2}}$ $\mathrm{B}_{1}=\frac{\mu_{\mathrm{o}} \mathrm{i}_{\mathrm{o}} \mathrm{x}}{2 \pi \mathrm{a}^{2}}$...(1) when $\mathrm{a}<\mathrm{x}<\mathrm{b}$ $\mathrm{B}_{2}(2 \pi \mathrm{x})=\mu_{0} \mathrm{i}_{\mathrm{o}}$ $\mathrm{B}_{2}=\frac{\mu_{\mathrm{o}} \mathrm{i}_{\mathrm{o}}}{2 \pi \mathrm{x}}$...(2) $\frac{\mathrm{B}_{1}}{\mathrm{~B}_{2}}=\frac{\mu_{\mathrm{o}} \mathrm{i}_{\mathrm{o}} \frac{\mathrm{x}}{2 \pi \mathrm{a}^{2}}}{\frac{\mu_{\mathrm{o}} \mathrm{i}_{\mathrm{o}}}{2 \pi \mathrm{x}}}=\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
