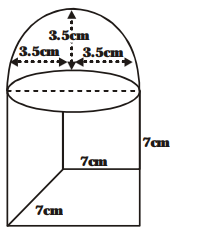
A cubical block of side 7 cm is surmounted by a hemisphere.

On 7 cm × 7 cm base of the cubical block, we can mount hemisphere having greatest diameter equal to 7 cm.

Here, the radius of the hemisphere = 3.5 cm.

Now, the surface area of the solid made in figure.

= The surface area of the cube + The curved surface area of the hemisphere – The area of the base of the hemisphere. 

$=\left\{6 \times(7)^{2}+2 \pi \times(3.5)^{2}-\pi \times(3.5)^{2}\right\} \mathrm{cm}^{2}$

( $\because$ the part of the top of the cubical part which is covered by the hemisphere is not visible outside)

$=\left\{6 \times 49+\frac{22}{7} \times \frac{35}{10} \times \frac{35}{10}\right\} \mathrm{cm}^{2}$

$=\left\{\mathbf{2 9 4}+\mathbf{1 1} \times \frac{\mathbf{3 5}}{\mathbf{1 0}}\right\} \mathrm{cm}^{2}=332.5 \mathrm{~cm}^{2}$