A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope.

Solution:

(i) $r=5 \mathrm{~m}, \theta=90^{\circ}$

The required area (Grazing area for horse)

$=$ The sector area of the sector $\mathrm{OAB}$

$=\frac{90}{360} \times \pi r^{2}=\frac{1}{4} \times 3.14 \times(5)^{2} \mathrm{~m}^{2}$

$=\frac{1}{4} \times 78.50 \mathrm{~m}^{2}=19.625 \mathrm{~m}^{2}$

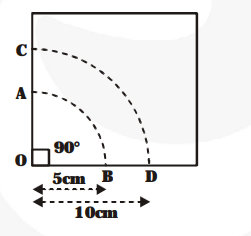
(ii) Now, the radius for the sector OCD = 10 m

and sector angle = 90°

The area of the sector OCD

$=\frac{\mathbf{9 0}}{\mathbf{3 6 0}} \times \pi \times(10)^{2} \mathrm{~m}^{2}=\frac{\mathbf{1}}{\mathbf{4}} \times 3.14 \times 100 \mathrm{~m}^{2}=78.5 \mathrm{~m}^{2}$

Therefore, the increase of grazing area

= The area of sector OCD

– The area of sector OAB

$=78.5 \mathrm{~m}^{2}-19.625 \mathrm{~m}^{2}$

$=58.875 \mathrm{~m}^{2}$