A hydraulic press can lift $100 \mathrm{~kg}$ when a mass ' $\mathrm{m}$ ' is placed on the smaller piston.
It can lift______ $\mathrm{kg}$ when the diameter of the larger piston is increased by 4 times and that of the smaller piston is decreased by 4 times keeping the same mass ' $m$ ' on the smaller piston.
$(25600)$
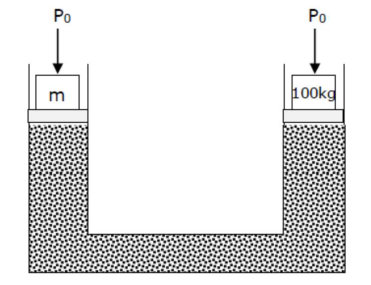
Atmospheric pressure $P_{0}$ will be acting on both the limbs of hydraulic lift.
Applying pascal's law for same liquid level
$\Rightarrow \mathrm{P}_{0}+\frac{\mathrm{mg}}{\mathrm{A}_{1}}=\mathrm{P}_{0}+\frac{(100) \mathrm{g}}{\mathrm{A}_{2}}$
$\Rightarrow \frac{\mathrm{Mg}}{\mathrm{A}_{1}}=\frac{(100) \mathrm{g}}{\mathrm{A}_{2}} \Rightarrow \frac{\mathrm{m}}{100}=\frac{\mathrm{A}_{1}}{\mathrm{~A}_{2}} \ldots(1)$
Diameter of piston on side of $100 \mathrm{~kg}$ is increased by 4 times so new area $=16 \mathrm{~A}_{2}$
Diameter of piston on side of $(\mathrm{m}) \mathrm{kg}$ is decreasing
$A_{1}=\frac{A_{1}}{16}$
(In order to increasing weight lifting capacity, diameter of smaller piston must be
reduced)
Again, $\frac{m g}{\left(\frac{A_{1}}{16}\right)}=\frac{M^{\prime} g}{16 A_{2}} \Rightarrow \frac{256 m}{M^{\prime}}=\frac{A_{1}}{A_{2}}$
From equation $(1)=\frac{256 \mathrm{~m}}{\mathrm{M}^{\prime}}=\frac{\mathrm{m}}{100} \Rightarrow \therefore \mathrm{M}^{\prime}=25600 \mathrm{~kg}$