A man goes 15 meters due west and then 8 meters due north. How far is he from the starting point?

Let us draw the diagram. Let A be the starting point. From point B he goes to the north.

Therefore, we obtained the following drawing.

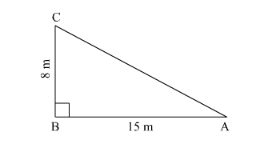
Now we have to find how far is he from the starting point that is we have to find $l(A C)$.

Now we will use Pythagoras theorem to find the length of $A C$.

$A C^{2}=A B^{2}+B C^{2}$....(1)

Let us substituting the values of AB and BC in equation (1) we get,

$A C^{2}=15^{2}+8^{2}$

$=225+64$

$=289$

Let us take the square root we get,

$A C=\pm \sqrt{289}$

$A C=\pm 17$

Since AC is the distance therefore it should be positive.

$\therefore A C=17 \mathrm{~m}$

Therefore, he is $17 \mathrm{~m}$ from the starting point.