A man goes 80 m due east and then 150 m due north.

Let the man starts from point A and goes 80 m due east to B.
Then, from B, he goes 150 m due north to C.

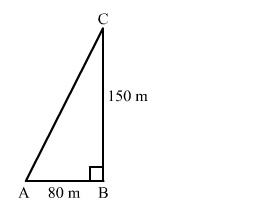
We need to find AC.
In right-angled triangle ABC, we have:

$A C^{2}=A B^{2}+B C^{2}$

$A C=\sqrt{80^{2}+150^{2}}$

$=\sqrt{6400+22500}$

$=\sqrt{28900}$

$=170 \mathrm{~m}$

Hence, the man is 170 m away from the starting point.