A student determined Young's Modulus of elasticity using the formula $\mathrm{Y}=\frac{\mathrm{MgL}^{3}}{4 \mathrm{bd}^{3} \delta}$. The value
of $\mathrm{g}$ is taken to be $9.8 \mathrm{~m} / \mathrm{s}^{2}$, without any significant error, his observation are as following.
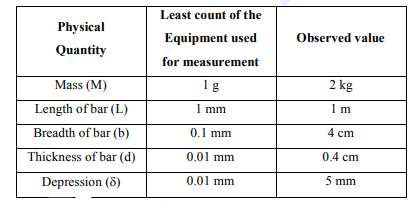
Then the fractional error in the measurement of $Y$ is:
Correct Option: , 2
$\mathrm{y}=\frac{\mathrm{MgL}^{3}}{4 \mathrm{bd}^{3} \delta}$
$\frac{\Delta \mathrm{y}}{\mathrm{y}}=\frac{\Delta \mathrm{M}}{\mathrm{M}}+\frac{3 \Delta \mathrm{L}}{\mathrm{L}}+\frac{\Delta \mathrm{b}}{\mathrm{b}}+\frac{3 \Delta \mathrm{d}}{\mathrm{d}}+\frac{\Delta \delta}{\delta}$
$\frac{\Delta y}{y}=\frac{10^{-3}}{2}+\frac{3 \times 10^{-3}}{1}+\frac{10^{-2}}{4}+\frac{3 \times 10^{-2}}{4}+\frac{10^{-2}}{5}$
$=10^{-3}[0.5+3+2.5+7.5+2]=0.0155$
Option (2)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
