Question:
A system consists of two identical spheres each of mass $1.5 \mathrm{~kg}$ and radius $50 \mathrm{~cm}$ at the end of light rod. The distance between the centres of the two spheres is $5 \mathrm{~m}$. What will be the moment of inertia of the system about an axis perpendicular to the rod passing through its midpoint?
Correct Option: , 3
Solution:
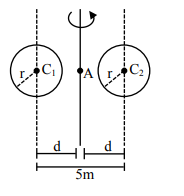
$\mathrm{M}=1.5 \mathrm{~kg}, \mathrm{r}=0.5 \mathrm{~m}, \mathrm{~d}=\frac{5}{2} \mathrm{~m}$
$\mathrm{I}=2\left(\frac{2}{5} \mathrm{Mr}^{2}+\mathrm{Md}^{2}\right)$
$=19.05 \mathrm{kgm}^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
