A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs 12 and Rs 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximize the profit?
Let x and y be the number of dolls of type A and B respectively that are produced per week.
The given problem can be formulated as follows.
Maximize $z=12 x+16 y$ (1)
subject to the constraints,
$x+y \leq 1200$ (2)
$y \leq \frac{x}{2} \Rightarrow x \geq 2 y$ (3)
$x-3 y \leq 600$ (4)
$x, y \geq 0$ (5)
The feasible region determined by the system of constraints is as follows.
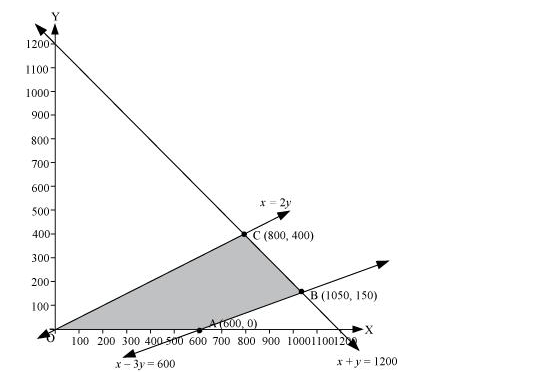
The corner points are A (600, 0), B (1050, 150), and C (800, 400).
The values of z at these corner points are as follows.
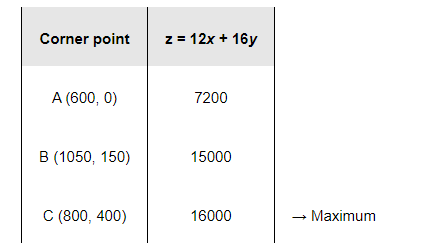
The maximum value of z is 16000 at (800, 400).
Thus, 800 and 400 dolls of type A and type B should be produced respectively to get the maximum profit of Rs 16000.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
