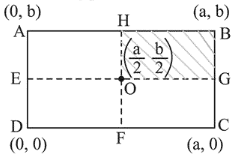
A uniform rectangular thin sheet $\mathrm{ABCD}$ of mass $\mathrm{M}$ has length a and breadth $b$, as shown in the figure. If the shaded portion HBGO is cut-off, the coordinates of the centre of mass of the remaining portion will be :
Correct Option: , 4
(4) With respect to point $\theta$, the $\mathrm{CM}$ of the cut-off portion
$\left(\frac{a}{4}, \frac{b}{4}\right)$
Using, $x_{\mathrm{CM}}=\frac{M X-m x}{M-m}$
$=\frac{M \times 0-\frac{M}{4} \times \frac{a}{4}}{M-\frac{M}{4}}=-\frac{a}{12}$
and $y_{C M}=-\frac{b}{12}$
So CM coordinates one
$x_{0}=\frac{a}{2}-\frac{a}{12}=\frac{5 a}{12}$'
and $y_{0}=\frac{b}{2}-\frac{b}{12}=\frac{5 b}{12}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
