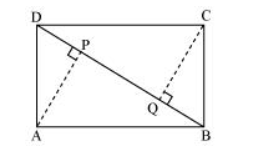
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that<br/><br/>(i) ΔAPB ≅ ΔCQD<br/><br/>(ii) AP = CQ

Solution:

(i) In $\triangle \mathrm{APB}$ and $\triangle \mathrm{CQD}$,

$\angle \mathrm{APB}=\angle \mathrm{CQD}\left(\right.$ Each $\left.90^{\circ}\right)$

$A B=C D$ (Opposite sides of parallelogram $A B C D$ )

$\angle A B P=\angle C D Q$ (Alternate interior angles for $A B \| C D$ )

$\therefore \triangle \mathrm{APB} \cong \triangle \mathrm{CQD}$ (By AAS congruency)

(ii) By using the above result

$\triangle \mathrm{APB} \cong \triangle \mathrm{CQD}$, we obtain

$\mathrm{AP}=\mathrm{CQ}(\mathrm{By} \mathrm{CPCT})$