ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q.

Given:
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q.

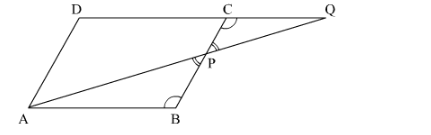
To Prove:  
The rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC. We need to prove that BP×DQ=AB×BC

Proof: 
In ∆ABP and ​ ∆QCP, we have
∠ABP = ​ ∠QCP                      (Alternate angles as AB || DC)
∠BPA = ​ ∠QPC                      ( Vertically opposite angles)
By AA similarity, we get
∆ABP ~ ∆QCP
We know that corresponding sides of similar triangles are proportional.

⇒ABQC=BPCP=APQP

⇒ABQC=BPCP⇒AB×CP=QC×BP

Adding AB×BP in both sides, we get

⇒AB×CP+AB×BP=QC×BP+AB×BP⇒AB×CP+BP=QC+AB×BP⇒AB×CP+BP=QC+CD×BP              

ABCD is a parallelogram, AB = CD⇒AB×BC=DQ×BP⇒BP×DQ=AB×BC