ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E.

Solution:



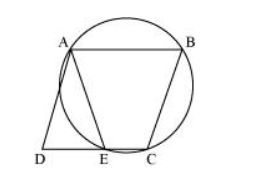
It can be observed that ABCE is a cyclic quadrilateral and in a cyclic quadrilateral, the sum of the opposite angles is 180°.

$\angle A E C+\angle C B A=180^{\circ}$

$\angle \mathrm{AEC}+\angle \mathrm{AED}=180^{\circ}($ Linear pair $)$

$\angle A E D=\angle C B A \ldots(1)$

For a parallelogram, opposite angles are equal.

$\angle \mathrm{ADE}=\angle \mathrm{CBA} \ldots(2)$

From $(1)$ and $(2)$,

$\angle \mathrm{AED}=\angle \mathrm{ADE}$

$A D=A E$ (Angles opposite to equal sides of a triangle)