ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively.

Solution:



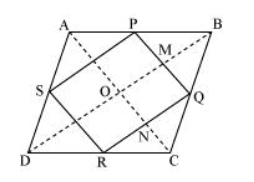
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.

$\therefore \mathrm{PQ} \| \mathrm{AC}$ and $\mathrm{PQ}=\frac{1}{2} \mathrm{AC}$ (Using mid-point theorem) $\ldots$(1)

In $\triangle \mathrm{ADC}$

$R$ and $S$ are the mid-points of $C D$ and $A D$ respectively.

$\therefore R S \| A C$ and $R S=\frac{1}{2} A C$ (Using mid-point theorem) $\ldots$(2)

From equations (1) and (2), we obtain

$P Q \| R S$ and $P Q=R S$

Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.

Let the diagonals of rhombus $A B C D$ intersect each other at point $O$.

In quadrilateral OMQN,

$\mathrm{MQ} \| \mathrm{ON}(\because \mathrm{PQ} \| \mathrm{AC})$

$\mathrm{QN} \| \mathrm{OM}(\because \mathrm{QR} \| \mathrm{BD})$

Therefore, OMQN is a parallelogram.

$\Rightarrow \angle \mathrm{MQN}=\angle \mathrm{NOM}$

$\Rightarrow \angle \mathrm{PQR}=\angle \mathrm{NOM}$

However, $\angle N O M=90^{\circ}$ (Diagonals of a rhombus are perpendicular to each other)

$\therefore \angle P Q R=90^{\circ}$

Clearly, $P Q R S$ is a parallelogram having one of its interior angles as $90^{\circ}$.

Hence, PQRS is a rectangle.