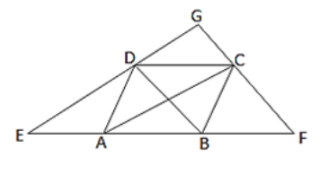
Question:
ABCD is a rhombus, EAFB is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles.
Solution:
We know that the diagonals of a rhombus are perpendicular bisector of each other.
∴ OA = OC, OB = OD, and ∠AOD = ∠COD = 90°
And ∠AOB = ∠COB = 90°
In ΔBDE, A and O are mid-points of BE and BD respectively.
OA ∥ DE
OC ∥ DG
In ΔCFA, B and O are mid-points of AF and AC respectively.
OB ∥ CF
OD ∥ GC
Thus, in quadrilateral DOGC, we have
OC ∥ DG and OD ∥ GC
⟹ DOCG is a parallelogram
∠DGC = ∠DOC
∠DGC = 90°
