An instructor has a question bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?
The given data can be tabulated as
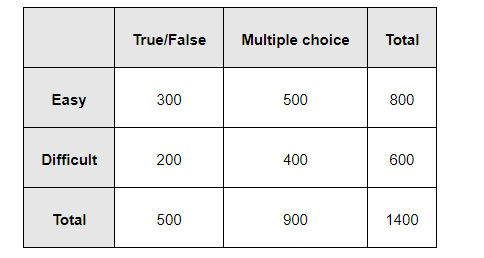
Let us denote E = easy questions, M = multiple choice questions, D = difficult questions, and T = True/False questions
Total number of questions = 1400
Total number of multiple choice questions = 900
Therefore, probability of selecting an easy multiple choice question is
$P(E \cap M)=\frac{500}{1400}=\frac{5}{14}$
Probability of selecting a multiple choice question, P (M), is
$\frac{900}{1400}=\frac{9}{14}$
P (E|M) represents the probability that a randomly selected question will be an easy question, given that it is a multiple choice question.
$\therefore \mathrm{P}(\mathrm{E} \mid \mathrm{M})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{M})}{\mathrm{P}(\mathrm{M})}=\frac{\frac{5}{14}}{\frac{9}{14}}=\frac{5}{9}$
Therefore, the required probability is $\frac{5}{9}$.