Balance the following redox reactions by ion-electron method:
(a) $\mathrm{MnO}_{4}^{-}$(aq) $+\mathrm{I}^{-}$(aq) $\rightarrow \mathrm{MnO}_{2}$ (s) $+\mathrm{I}_{2}$ (s) (in basic medium)
(b) $\mathrm{MnO}_{4}^{-}$(aq) $+\mathrm{SO}_{2}(\mathrm{~g}) \rightarrow \mathrm{Mn}^{2+}(\mathrm{aq})+\mathrm{HSO}_{4}^{-}$(aq) (in acidic solution)
(c) $\mathrm{H}_{2} \mathrm{O}_{2}$ (aq) $+\mathrm{Fe}^{2+}$ (aq) $\rightarrow \mathrm{Fe}^{3+}$ (aq) $+\mathrm{H}_{2} \mathrm{O}$ (I) (in acidic solution)
(d) $\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}+\mathrm{SO}_{2}(\mathrm{~g}) \rightarrow \mathrm{Cr}^{3+}(\mathrm{aq})+\mathrm{SO}_{4}^{2-}(\mathrm{aq})($ in acidic solution $)$
(a) Step 1: The two half reactions involved in the given reaction are:
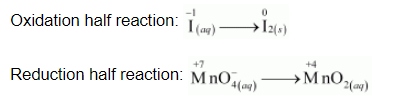
Step 2:
Balancing I in the oxidation half reaction, we have:
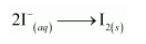
Now, to balance the charge, we add 2 e– to the RHS of the reaction.
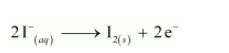
Step 3:
In the reduction half reaction, the oxidation state of Mn has reduced from +7 to +4. Thus, 3 electrons are added to the LHS of the reaction.
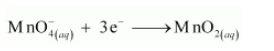
Now, to balance the charge, we add 4 OH– ions to the RHS of the reaction as the reaction is taking place in a basic medium.
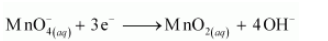
Step 4:
In this equation, there are 6 O atoms on the RHS and 4 O atoms on the LHS. Therefore, two water molecules are added to the LHS.
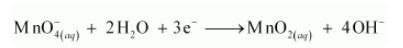
Step 5:
Equalising the number of electrons by multiplying the oxidation half reaction by 3 and the reduction half reaction by 2, we have:
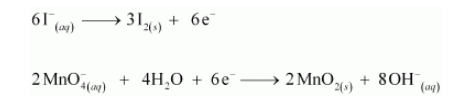
Step 6:
Adding the two half reactions, we have the net balanced redox reaction as:
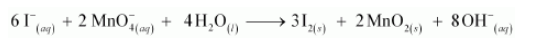
(b)Following the steps as in part (a), we have the oxidation half reaction as:

And the reduction half reaction as:
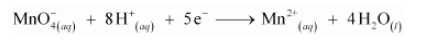
Multiplying the oxidation half reaction by 5 and the reduction half reaction by 2, and then by adding them, we have the net balanced redox reaction as:
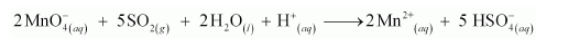
(c) Following the steps as in part (a), we have the oxidation half reaction as:
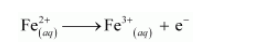
And the reduction half reaction as:
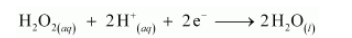
Multiplying the oxidation half reaction by 2 and then adding it to the reduction half reaction, we have the net balanced redox reaction as:
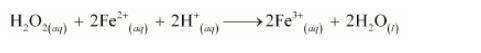
(d) Following the steps as in part (a), we have the oxidation half reaction as:
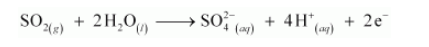
And the reduction half reaction as:
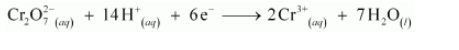
Multiplying the oxidation half reaction by 3 and then adding it to the reduction half reaction, we have the net balanced redox reaction as:
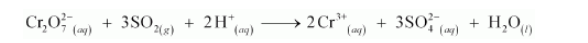
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
