Question.
Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.
Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.
Solution:
For the Balmer series, $n_{i}=2$. Thus, the expression of wavenumber $(\bar{v})$ is given by,
$\bar{v}=\left[\frac{1}{(2)^{2}}-\frac{1}{n_{\mathrm{f}}^{2}}\right]\left(1.097 \times 10^{7} \mathrm{~m}^{-1}\right)$
Wave number $(\bar{v})$ is inversely proportional to wavelength of transition. Hence, for the
longest wavelength transition, $(\bar{v})$ as to be the smallest.
For $(\bar{v})$ to be minimum, $n_{f}$ should be minimum.
For the Balmer series, a transition from $n_{i}=2$ to $n_{f}=3$ is allowed.
Hence, taking $n_{\mathrm{f}}=3$, we get:
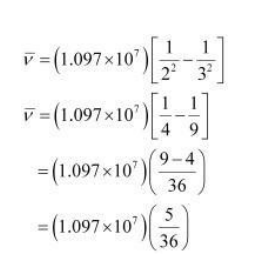
$\bar{v}=1.5236 \times 10^{6} \mathrm{~m}^{-1}$
For the Balmer series, $n_{i}=2$. Thus, the expression of wavenumber $(\bar{v})$ is given by,
$\bar{v}=\left[\frac{1}{(2)^{2}}-\frac{1}{n_{\mathrm{f}}^{2}}\right]\left(1.097 \times 10^{7} \mathrm{~m}^{-1}\right)$
Wave number $(\bar{v})$ is inversely proportional to wavelength of transition. Hence, for the
longest wavelength transition, $(\bar{v})$ as to be the smallest.
For $(\bar{v})$ to be minimum, $n_{f}$ should be minimum.
For the Balmer series, a transition from $n_{i}=2$ to $n_{f}=3$ is allowed.
Hence, taking $n_{\mathrm{f}}=3$, we get:
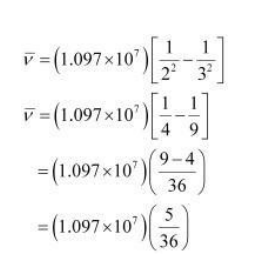
$\bar{v}=1.5236 \times 10^{6} \mathrm{~m}^{-1}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
