Question.
Construct a triangle $P Q R$ in which $Q R=6 \mathrm{~cm}, \angle Q=60^{\circ}$ and $P R-P Q=2 \mathrm{~cm}$
Solution:
The below given steps will be followed to construct the required triangle.
Step I: Draw line segment $Q R$ of $6 \mathrm{~cm}$. At point $Q$, draw an angle of $60^{\circ}$, say $\angle X Q R$.
Step II: Cut a line segment $Q S$ of $2 \mathrm{~cm}$ from the line segment $Q T$ extended in the opposite side of line segment $X Q$. (As PR > PQ and PR $P Q=2 \mathrm{~cm})$. Join SR.
Step III: Draw perpendicular bisector $A B$ of line segment $S R$. Let it intersect $Q X$ at point $P$. Join $P Q, P R$.
$\triangle \mathrm{PQR}$ is the required triangle.
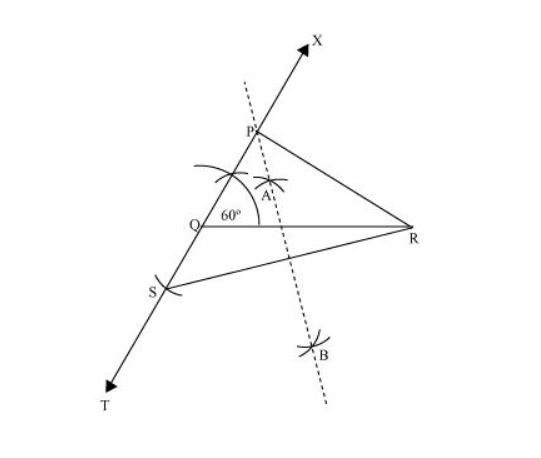
The below given steps will be followed to construct the required triangle.
Step I: Draw line segment $Q R$ of $6 \mathrm{~cm}$. At point $Q$, draw an angle of $60^{\circ}$, say $\angle X Q R$.
Step II: Cut a line segment $Q S$ of $2 \mathrm{~cm}$ from the line segment $Q T$ extended in the opposite side of line segment $X Q$. (As PR > PQ and PR $P Q=2 \mathrm{~cm})$. Join SR.
Step III: Draw perpendicular bisector $A B$ of line segment $S R$. Let it intersect $Q X$ at point $P$. Join $P Q, P R$.
$\triangle \mathrm{PQR}$ is the required triangle.

Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
