Find the area of a quadrilateral ABCD in which AB = 3 cm

Solution:



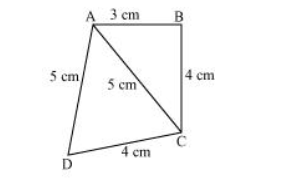
For $\triangle \mathrm{ABC}$,

$A C^{2}=A B^{2}+B C^{2}$

$(5)^{2}=(3)^{2}+(4)^{2}$

Therefore, $\triangle \mathrm{ABC}$ is a right-angled triangle, right-angled at point $\mathrm{B}$.

Area of $\triangle \mathrm{ABC}=\frac{1}{2} \times \mathrm{AB} \times \mathrm{BC}=\frac{1}{2} \times 3 \times 4=6 \mathrm{~cm}^{2}$

For $\triangle \mathrm{ADC}$,

Perimeter $=2 s=A C+C D+D A=(5+4+5) \mathrm{cm}=14 \mathrm{~cm}$

$s=7 \mathrm{~cm}$

By Heron's formula,

Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$

Area of $\Delta \mathrm{ADC}=[\sqrt{7(7-5)(7-5)(7-4)}] \mathrm{cm}^{2}$

$=(\sqrt{7 \times 2 \times 2 \times 3}) \mathrm{cm}^{2}$

$=2 \sqrt{21} \mathrm{~cm}^{2}$

$=(2 \times 4.583) \mathrm{cm}^{2}$

$=9.166 \mathrm{~cm}^{2}$

Area of $A B C D=$ Area of $\triangle A B C+$ Area of $\triangle A C D$

$=(6+9.166) \mathrm{cm}^{2}=15.166 \mathrm{~cm}^{2}=15.2 \mathrm{~cm}^{2}$ (approximately)