Question:
Find the equation of a plane which is at a distance 3√3 units from origin and the normal to which is equally inclined to coordinate axis.
Solution:
As the normal to the plane is equally inclined to the axes we have,
cos α = cos β = cos γ
So, cos2 α + cos2 α + cos2 α = 1
3 cos2 α = 1 ⇒ cos α = ± 1/√3
And, cos α = cos β = cos γ = ± 1/√3
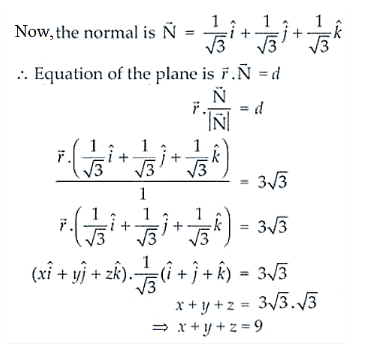
Thus, the equation of the plane is x + y + z = 9
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
