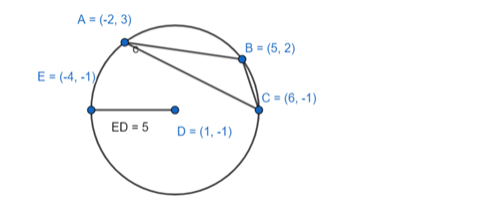
Find the equation of the circle which is circumscribed about the triangle

The general equation of a circle: $(x-h)^{2}+(y-k)^{2}=r^{2}$

$\ldots(\mathrm{i})$, where $(\mathrm{h}, \mathrm{k})$ is the centre and $\mathrm{r}$ is the radius.

Putting $A(-2,3), B(5,2)$ and $c(6,-1)$ in (i) we get

$h^{2}+k^{2}+4 h-6 k+13=r^{2} \ldots$ (ii)

$h^{2}+k^{2}-10 h-4 k+29=r^{2} \ldots$ (iii)and

$h^{2}+k^{2}-12 h+2 k+37=r^{2} \ldots$ (iv)

subtracting (ii) from (iii) and also from (iv),

$-14 h+2 k+16=0 \Rightarrow-7 h+k+8=0$

$-16 h+8 k+24=0 \Rightarrow-2 h+k+3=0$

Subtracting,

$5 h-5=0 \Rightarrow h=1$

$k=-1$

Centre $=(1,-1)$

Putting these values in (ii) we get, radius

$=\sqrt{1+1+4+6+13}=\sqrt{25}=5$

Equation of the circle is

$(x-1)^{2}+\{y-(-1)\}^{2}=5^{2}$

$(x-1)^{2}+(y+1)^{2}=25$