Find the equation of the hyperbola whose foci are

Given: Foci are (0, ±13), the conjugate axis is of the length 24

Need to find: The equation of the hyperbola.

Let, the equation of the hyperbola be:

$\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1$

The conjugate axis is of the length 24 , i.e., $2 \mathrm{~b}=24$

Therefore, $b=12$

The foci are given at $(0, \pm 13)$

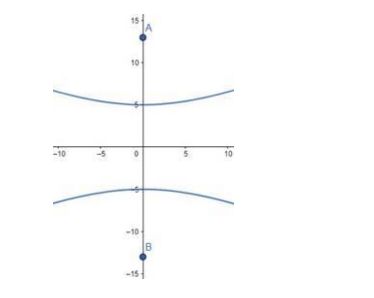
$\mathrm{A}$ and $\mathrm{B}$ are the foci.

That means, ae $=13$, where e is the eccentricity.

We know that,

$e=\sqrt{1+\frac{b^{2}}{a^{2}}}$

Therefore,

$\Rightarrow \sqrt{1+\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}}=13$

$\Rightarrow a \frac{\sqrt{a^{2}+b^{2}}}{a}=13$

$\Rightarrow \mathrm{a}^{2}+\mathrm{b}^{2}=169$ [Squaring both sides]

$\Rightarrow \mathrm{a}^{2}=169-\mathrm{b}^{2}=169-144=25[$ As $\mathrm{b}=12]$

So, the equation of the hyperbola is,

$\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1 \Rightarrow \frac{y^{2}}{25}-\frac{x^{2}}{144}=1[$ Answer $]$