Find the equation of the line through the intersection of the lines

Suppose the given two lines intersect at a point $P\left(x_{1}, y_{1}\right) .$ Then, $\left(x_{1}, y_{1}\right)$ satisfies each of the given equations.

$2 x-3 y+1=0 \ldots$ (i)

$x+y-2=0 \ldots$ (ii)

Now, we find the point of intersection of eq. (i) and (ii)

Multiply the eq. (ii) by 2 , we get

$2 x+2 y-4=0 \ldots$ (iii)

On subtracting eq. (iii) from (i), we get

$2 x-3 y+1-2 x-2 y+4=0$

$\Rightarrow-5 y+5=0$

$\Rightarrow-5 y=-5$

$\Rightarrow y=1$

Putting the value of y in eq. (ii), we get

$x+1-2=0$

$\Rightarrow x-1=0$

$\Rightarrow x=1$

Hence, the point of intersection $P\left(x_{1}, y_{1}\right)$ is $(1,1)$

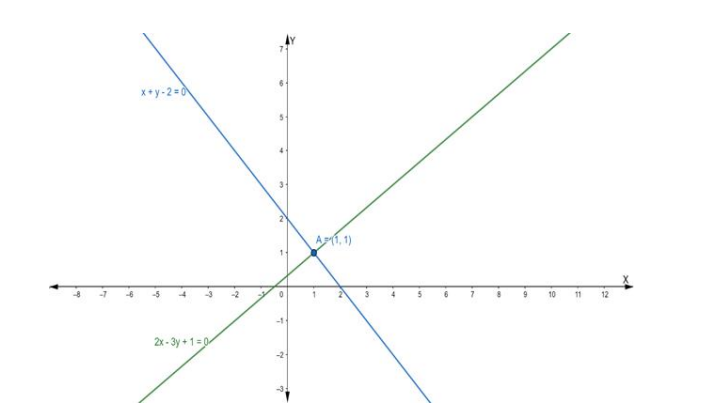
The equation of a line parallel to $\mathrm{y}$-axis is of the form

$x=a$ where $a$ is some constant 

Given that this equation of the line passing through the point of intersection (1, 1)

Hence, point (1, 1) will satisfy the equation of a line.

Putting x = 1 in the equation y = b, we get

$x=a$

$\Rightarrow 1=\mathrm{a}$

or $a=1$

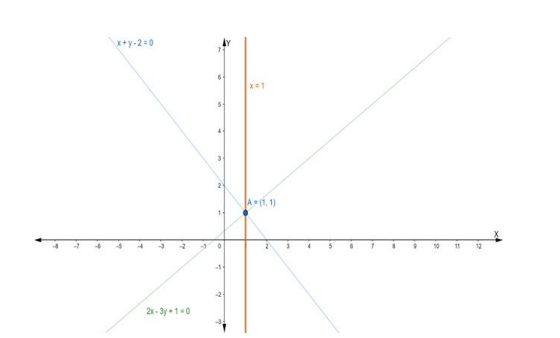
Now, required equation of line is $x=1$