Find the equations of the two lines through the origin

Solution:

Any point in the given line is

x – 3/ 2 = y – 3/1 = z/1 = λ

x = 2λ + 3, y = λ + 3 and z = λ

Let it be the coordinates of P

So, the direction ratios of OP are (2λ + 3 – 0), (λ + 3 – 0) and (λ – 0) ⇒ 2λ + 3, λ + 3, λ

But the direction ratios of the line PQ are 2, 1, 1

Now, we know that

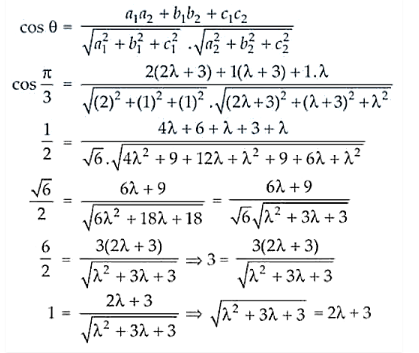
λ2 + 3λ + 3 = 4λ2 + 9 + 12λ (On squaring on both sides)

3λ2 + 9λ + 6 = 0

λ2 + 3λ + 2 = 0

(λ + 1)( λ + 2) = 0

λ = -1, -2

So, the direction are:

[2(-1) + 3, -1 + 3, -1] = (-2, 2, -1) when λ = -1 and

 

[2(-2) + 3, -2 + 3, -2] = (-1, 1, -2) when λ = -2.

 

Thus, the required equation of planes are

x/1 = y/2 = z/-1 and x/-1 = y/1 = z/-2