Find the foot of perpendicular from

Given, 

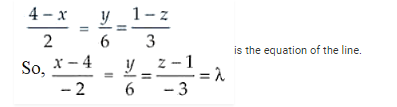
Now, the coordinates of any point Q on the line are

x = -2λ + 4, y = 6λ and z = -3λ + 1 and the given point is P(2, 3, -8)

The direction ratios of PQ are -2λ + 4 – 2, 6λ – 3, -3λ + 1 + 8 i.e. -2λ + 2, 6λ – 3, -3λ + 9

And the direction ratios of the given line are -2, 6, -3.

If PQ ⊥ line, then

-2(-2λ + 2) + 6(6λ – 3) – 3(-3λ + 9) = 0

4λ – 4 + 36λ – 18 + 9λ – 27 = 0

49λ – 49 = 0

λ = 1

Now, the foot of the perpendicular is -2(1) + 4, 6(1), -3(1) + 1 i.e. 2, 6, -2

Hence, the distance PQ is

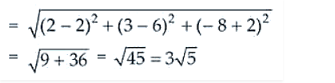
Thus, the required coordinates of the foot of perpendicular are 2, 6, -2 and the required distance is 3√5 units.