Question:
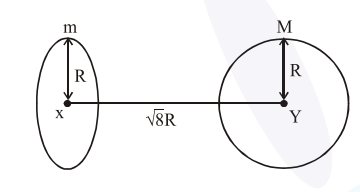
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If
$\sqrt{8} \mathrm{R}$ is the distance between the centres of a ring (of mass ' $m$ ') and a sphere (mass 'M') where both have equal radius 'R'.
Correct Option: , 4
Solution:
Gravitational field of ring
$=-\frac{\mathrm{Gmx}}{\left(\mathrm{R}^{2}+\mathrm{x}^{2}\right)^{3 / 2}}$
Force between sphere \& ring
$=\frac{\operatorname{GmM}(\sqrt{8} \mathrm{R})}{\left(\mathrm{R}^{2}+8 \mathrm{R}^{2}\right)^{3 / 2}}$
$=\frac{G m M}{R^{2}} \times \frac{\sqrt{8}}{27}$