Find the probability distribution of
(i) number of heads in two tosses of a coin
(ii) number of tails in the simultaneous tosses of three coins
(iii) number of heads in four tosses of a coin
(i) When one coin is tossed twice, the sample space is
{HH, HT, TH, TT}
Let X represent the number of heads.
∴ X (HH) = 2, X (HT) = 1, X (TH) = 1, X (TT) = 0
Therefore, X can take the value of 0, 1, or 2.
It is known that,
$\mathrm{P}(\mathrm{HH})=\mathrm{P}(\mathrm{HT})=\mathrm{P}(\mathrm{TH})=\mathrm{P}(\mathrm{TT})=\frac{1}{4}$
$P(X=0)=P(T T)=\frac{1}{4}$
$P(X=1)=P(H T)+P(T H)=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$
$\mathrm{P}(\mathrm{X}=2)=\mathrm{P}(\mathrm{HH})=\frac{1}{4}$
Thus, the required probability distribution is as follows.
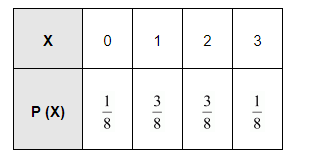
(iii) When a coin is tossed four times, the sample space is
$\mathrm{S}=\left\{\begin{array}{c}\mathrm{HHHH}, \mathrm{HHHT}, \mathrm{HHTH}, \mathrm{HHTT}, \mathrm{HTHT}, \mathrm{HTHH}, \mathrm{HTTH}, \mathrm{HTTT}, \\ \mathrm{THHH}, \mathrm{THHT}, \mathrm{THTH}, \mathrm{THTT}, \mathrm{TTHH}, \mathrm{TTHT}, \mathrm{TTTH}, \mathrm{TTTT}\end{array}\right\}$
Let X be the random variable, which represents the number of heads.
It can be seen that X can take the value of 0, 1, 2, 3, or 4
$P(X=0)=P(T T T T)=\frac{1}{16}$
P (X = 1) = P (TTTH) + P (TTHT) + P (THTT) + P (HTTT)
$=\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}=\frac{4}{16}=\frac{1}{4}$
P (X = 2) = P (HHTT) + P (THHT) + P (TTHH) + P (HTTH) + P (HTHT)
+ P (THTH)
$=\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}=\frac{6}{16}=\frac{3}{8}$
P (X = 3) = P (HHHT) + P (HHTH) + P (HTHH) P (THHH)
$=\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}=\frac{4}{16}=\frac{1}{4}$
$P(X=4)=P(\mathrm{HHHH})=\frac{1}{16}$
Thus, the probability distribution is as follows.
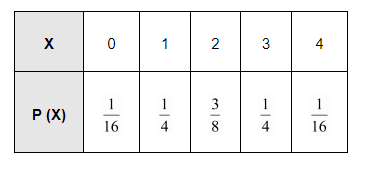
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
