Find the values of the following expressions:

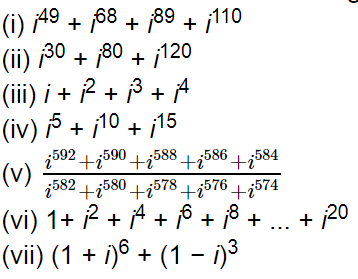
(i) $i^{49}+i^{68}+i^{89}+i^{110}$

$=i^{4 \times 12+1}+i^{4 \times 17}+i^{4 \times 22+1}+i^{4 \times 27+2}$

$=\left\{\left(i^{4}\right)^{12} \times i\right\}+\left\{\left(i^{4}\right)^{17}\right\}+\left\{\left(i^{4}\right)^{22} \times i\right\}+\left\{\left(i^{4}\right)^{27} \times i^{2}\right\}$

$=i+1+i+i^{2} \quad\left[\because i^{4}=1\right]$

$=2 i+1-1 \quad\left[\because i^{2}=-1\right]$

$=2 i$

(ii) $i^{30}+i^{80}+i^{120}$

$=i^{4 \times 7+2}+i^{4 \times 20}+i^{4 \times 30}$

$=\left\{\left(i^{4}\right)^{7} \times i^{2}\right\}+\left\{\left(i^{4}\right)^{20}\right\}+\left\{\left(i^{4}\right)^{30}\right\}$

$=i^{2}+1+1 \quad\left[\because i^{4}=1\right]$

$=-1+2 \quad\left[\because i^{2}=-1\right]$

= 1

(iii) $i+i^{2}+i^{3}+i^{4}$

$=i-1-i+1 \quad\left[\because i^{2}=-1, i^{3}=-i\right.$ and $\left.i^{4}=1\right]$

= 0

(iv) $i^{5}+i^{10}+i^{15}$

$=i^{4 \times 1+1}+i^{4 \times 2+2}+i^{4 \times 3+3}$

$=\left\{\left(i^{4}\right)^{1} \times i\right\}+\left\{\left(i^{4}\right)^{2} \times i^{2}\right\}+\left\{\left(i^{4}\right)^{3} \times i^{3}\right\}$

$=i+i^{2}+i^{3} \quad\left[\because i^{4}=1\right]$

$=i-1-i \quad\left[\because i^{2}=-1, i^{3}=-i\right]$

= -1

$(\mathbf{V}) \frac{i^{592}+i^{590}+i^{588}+i^{586}+i^{584}}{i^{582}+i^{580}+i^{578}+i^{576}+i^{574}}$

$=\frac{i^{4 \times 148}+i^{4 \times 147+2}+i^{4 \times 147}+i^{4 \times 146+2}+i^{4 \times 146}}{i^{4 \times 145+2}+i^{4 \times 145}+i^{4 \times 144+2}+i^{4 \times 144}+i^{4 \times 143+2}}$

$=\frac{\left(i^{4}\right)^{148}+\left\{\left(i^{4}\right)^{147} \times i^{2}\right\}+\left\{\left(i^{4}\right)^{146}\right\}+\left\{\left(i^{4}\right)^{146} \times i^{2}\right\}+\left\{\left(i^{4}\right)^{146}\right\}}{\left\{\left(i^{4}\right)^{145} \times i^{2}\right\}+\left\{\left(i^{4}\right)^{145}\right\}+\left\{\left(i^{4}\right)^{144} \times i^{2}\right\}+\left\{\left(i^{4}\right)^{144}\right\}+\left\{\left(i^{4}\right)^{143} \times i^{2}\right\}}$

$=\frac{1+i^{2}+1+i^{2}+1}{i^{2}+1+i^{2}+1+i^{2}} \quad\left[\because i^{4}=1\right]$

$=\frac{1-1+1-1+1}{-1+1-1+1-1} \quad\left[\because i^{2}=-1\right]$

= -1

(vi) $1+i^{2}+i^{4}+i^{6}+i^{8}+\ldots+i^{20}$

$\because i^{2}=-1$

$i^{4}=1$

$i^{6}=-1$

$i^{8}=1$

$i^{20}=1$

$\therefore 1+i^{2}+i^{4}+i^{6}+i^{8}+\ldots+i^{20}$

$=[1+(-1)]+[1+(-1)]+[1+(-1)]+\ldots+[1+(-1)]+1$

$=5 \times[1+(-1)]+1$     $[$ As, there are 11 terms $]$

$=5 \times 0+1$

$=1$

(vii) $(1+i)^{6}+(1-i)^{3}$

$=\left[(1+i)^{2}\right]^{3}+(1-i)^{3}$

$=\left[1^{2}+i^{2}+2 i\right]^{3}+\left(1^{3}-i^{3}+3 i^{2}-3 i\right)$

$=[1-1+2 i]^{3}+(1+i-3-3 i) \quad\left[\because i^{2}=-1, i^{3}=-1\right]$

$=(2 i)^{3}+(-2-2 i)$

$=8 i^{3}-2-2 i$

$=-8 i-2-2 i$              $\left[\because i^{3}=-i\right]$

$=-10 i-2$