Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
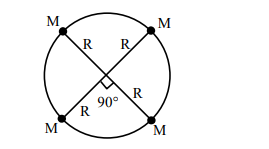
Correct Option: , 2
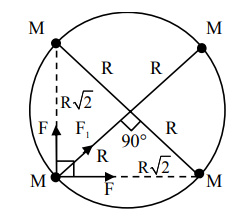
$\mathrm{F}_{\mathrm{net}}=\frac{\mathrm{MV}^{2}}{\mathrm{R}}$
$\sqrt{2} \mathrm{~F}+\mathrm{F}_{1}=\frac{\mathrm{MV}^{2}}{\mathrm{R}}$
$\sqrt{2} \frac{\mathrm{GMM}}{(\sqrt{2} \mathrm{R})^{2}}+\frac{\mathrm{GMM}}{(2 \mathrm{R})^{2}}=\frac{\mathrm{MV}^{2}}{\mathrm{R}}$
$\frac{\mathrm{GM}}{\mathrm{R}}\left(\frac{1}{\sqrt{2}}+\frac{1}{4}\right)=\mathrm{V}^{2}$
$\frac{\mathrm{GM}}{\mathrm{R}}\left(\frac{4+\sqrt{2}}{4 \sqrt{2}}\right)=\mathrm{V}^{2}$
$\mathrm{V}=\sqrt{\frac{\mathrm{GM}(4+\sqrt{2})}{\mathrm{R} 4 \sqrt{2}}}$
$\mathrm{~V}=\frac{1}{2} \sqrt{\frac{\mathrm{GM}(2 \sqrt{2}+1)}{\mathrm{R}}}$
Option (2)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
