Four point charges $q_{A}=2 \mu C, q_{B}=-5 \mu C, q_{C}=2 \mu C$, and $q_{D}=-5 \mu C$ are located at the corners of a square ABCD of side $10 \mathrm{~cm}$. What is the force on a charge of $1 \mu \mathrm{C}$ placed at the centre of the square?
The given figure shows a square of side 10 cm with four charges placed at its corners. O is the centre of the square
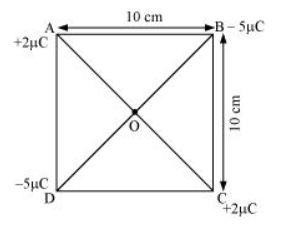
Where,
(Sides) AB = BC = CD = AD = 10 cm
(Diagonals) $A C=B D=10 \sqrt{2} \mathrm{~cm}$
$A O=O C=D O=O B=5 \sqrt{2} \mathrm{~cm}$
A charge of amount 1μC is placed at point O.
Force of repulsion between charges placed at corner A and centre O is equal in magnitude but opposite in direction relative to the force of repulsion between the charges placed at corner C and centre O. Hence, they will cancel each other. Similarly, force of attraction between charges placed at corner B and centre O is equal in magnitude but opposite in direction relative to the force of attraction between the charges placed at corner D and centre O. Hence, they will also cancel each other. Therefore, net force caused by the four charges placed at the corner of the square on 1 μC charge at centre O is zero.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
