If (a2+b2)x2+2(ab+bd)x+c2+d2=0 has no real roots, then

The given quadric equation is $\left(a^{2}+b^{2}\right) x^{2}+2(a b+b d) x+c^{2}+d^{2}=0$, and roots are equal.

Here, $a=\left(a^{2}+b^{2}\right), b=2(a b+b d)$ and, $c=c^{2}+d^{2}$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=\left(a^{2}+b^{2}\right), b=2(a b+b d)$ and, $c=c^{2}+d^{2}$

$=\{2(a b+b d)\}^{2}-4 \times\left(a^{2}+b^{2}\right) \times\left(c^{2}+d^{2}\right)$

$=4 a^{2} b^{2}+4 b^{2} d^{2}+8 a b^{2} d-4\left(a^{2} c^{2}+a^{2} d^{2}+b^{2} c^{2}+b^{2} d^{2}\right)$

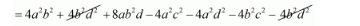
$=4 a^{2} b^{2}+8 a b^{2} d-4 a^{2} c^{2}-4 a^{2} d^{2}-4 b^{2} c^{2}$

$=4\left(a^{2} b^{2}+2 a b^{2} d-a^{2} c^{2}-a^{2} d^{2}-b^{2} c^{2}\right)$

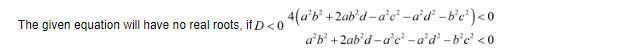
$a d \neq b c$

Thus, the correct answer is (d)