If ∆ABC is a right triangle such that ∠C = 90°,

We are given the following information in the form of the triangle

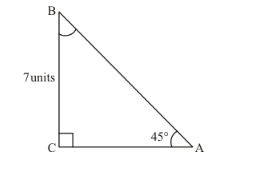
It is required to find $\angle B$ and length of sides $A B$ and $A C$

In $\triangle A B C \angle C=90^{\circ}$

Now we know that sum of all the angles of any triangle is $180^{\circ}$

Therefore,

$\angle A+\angle B+\angle C=180^{\circ}$.....(1)

Now by substituting the values of known angles $\angle A$ and $\angle C$ in equation (1)

We get,

$45^{\circ}+\angle B+90^{\circ}=180^{\circ}$

Therefore,

$\angle B+135^{\circ}=180^{\circ}$

$\Rightarrow \quad \angle B=180^{\circ}-135^{\circ}$

$\Rightarrow \quad \angle B=45^{\circ}$

Therefore,

$\angle B=45^{\circ} \ldots \ldots(2)$

Now,

We know that,

$\cos B=\cos 45^{\circ}$

$\Rightarrow \frac{B C}{A B}=\cos 45^{\circ}$.....(3)

Now we have,

$B C=7$ units and $\cos 45^{\circ}=\frac{1}{\sqrt{2}}$

Therefore by substituting above values in equation (3)

We get,

$\cos B=\cos 45^{\circ}$

$\Rightarrow \frac{7}{A B}=\cos 45^{\circ}$

$\Rightarrow \frac{7}{A B}=\frac{1}{\sqrt{2}}$

Now by cross multiplying we get,

$7 \sqrt{2}=A B$

$\Rightarrow A B=7 \sqrt{2}$

Therefore,

$A B=7 \sqrt{2}$ units.....(4)

Now,

We know that,

$\sin B=\sin 45^{\circ}$

$\Rightarrow \frac{A C}{A B}=\sin 45^{\circ}$....(5)

Now we have,

$A B=7 \sqrt{2}$ units and $\sin 45^{\circ}=\frac{1}{\sqrt{2}}$

Therefore by substituting above values in equation (5)

We get,

$\frac{A C}{7 \sqrt{2}}=\sin 45^{\circ}$

$\Rightarrow \frac{A C}{7 \sqrt{2}}=\frac{1}{\sqrt{2}}$

Now by cross multiplying we get,

$A C=\frac{7 \sqrt{2}}{\sqrt{2}}$

$\Rightarrow A C=7$

Therefore,

$A C=7$ units....(6)

Therefore,

From equation (2), (4) and (6)

$\angle B=45^{\circ}, A B=7 \sqrt{2}$ units,$A C=7$ units