If PT is a tangent at T to a circle whose centre is O and OP = 17 cm,

Let us put the given data in the form of a diagram.

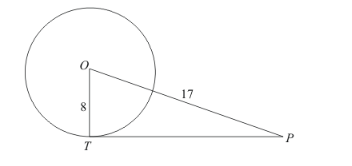
We have to find TP. From the properties of tangents we know that a tangent will always be at right angles to the radius of the circle at the point of contact. Therefore is a right angle and triangle OTP is a right triangle.

We can find the length of TP using Pythagoras theorem. We have,

$T P^{2}=O P^{2}-O T^{2}$

$T P^{2}=17^{2}-8^{2}$

$T P^{2}=(17-8)(17+8)$

$T P^{2}=9 \times 25$

$T P^{2}=225$

$T P=\sqrt{225}$

$T P=15$