Question:
If the sum of the zeros of the quadratic polynomial $l(t)=k t^{2}+2 t+3 k$ is equal to their product, find the value of $k$.
Solution:
Let $\alpha, \beta$ be the zeros of the polynomial $f(t)=k t^{2}+2 t+3 k$. Then,
$\alpha+\beta=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$\alpha+\beta=\frac{-2}{k}$
$\alpha \beta=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
$\alpha \beta=\frac{3 k}{k}$
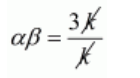
$\alpha \beta=3$
It is given that the sum of the zero of the quadratic polynomial is equal to their product then, we have
$\alpha+\beta=\alpha \beta$
$\frac{-2}{k}=3$
$-2=3 \times k$
$\frac{-2}{3}=k$
Hence, the value of $k$ is $\frac{-2}{3}$