Question.
If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution:
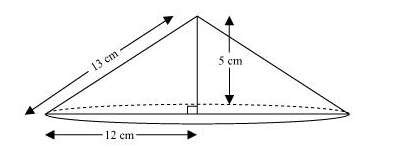
When right-angled $\triangle A B C$ is revolved about its side $5 \mathrm{~cm}$, a cone will be formed having radius $(r)$ as $12 \mathrm{~cm}$, height $(h)$ as $5 \mathrm{~cm}$, and slant height ( $l$ ) as $13 \mathrm{~cm}$.
Volume of cone $=\frac{1}{3} \pi r^{2} h$
$=\left[\frac{1}{3} \times \pi \times(12)^{2} \times 5\right] \mathrm{cm}^{3}$
$=240 \pi \mathrm{cm}^{3}$
Therefore, the volume of the cone so formed is $240 \pi \mathrm{cm}^{3}$.
Required ratio $=\frac{100 \pi}{240 \pi}$
$=\frac{5}{12}=5: 12$
When right-angled $\triangle A B C$ is revolved about its side $5 \mathrm{~cm}$, a cone will be formed having radius $(r)$ as $12 \mathrm{~cm}$, height $(h)$ as $5 \mathrm{~cm}$, and slant height ( $l$ ) as $13 \mathrm{~cm}$.
Volume of cone $=\frac{1}{3} \pi r^{2} h$
$=\left[\frac{1}{3} \times \pi \times(12)^{2} \times 5\right] \mathrm{cm}^{3}$
$=240 \pi \mathrm{cm}^{3}$
Therefore, the volume of the cone so formed is $240 \pi \mathrm{cm}^{3}$.
Required ratio $=\frac{100 \pi}{240 \pi}$
$=\frac{5}{12}=5: 12$