Question:
If three of the six vertices of a regular hexagon are chosen at random, then the probability that the triangle formed with these chosen vertices is equilateral is :
Correct Option: , 2
Solution:
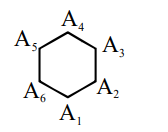
Only two equilateral tringles are possible $\mathrm{A}_{1} \mathrm{~A}_{3}$
$\mathrm{A}_{5}$ and $\mathrm{A}_{2} \mathrm{~A}_{5} \mathrm{~A}_{6}$
$\frac{2}{6_{C_{2}}}=\frac{2}{20}=\frac{1}{10}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
