Question.
If two circles intersect at two points, then prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
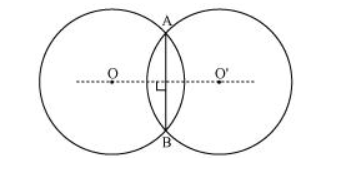
Consider two circles centered at point O and O’, intersecting each other at point A and B respectively.
Join AB. AB is the chord of the circle centered at O. Therefore, perpendicular bisector of AB will pass through O.
Again, AB is also the chord of the circle centered at O’. Therefore, perpendicular bisector of AB will also pass through O’.
Clearly, the centres of these circles lie on the perpendicular bisector of the common chord.
Consider two circles centered at point O and O’, intersecting each other at point A and B respectively.
Join AB. AB is the chord of the circle centered at O. Therefore, perpendicular bisector of AB will pass through O.
Again, AB is also the chord of the circle centered at O’. Therefore, perpendicular bisector of AB will also pass through O’.
Clearly, the centres of these circles lie on the perpendicular bisector of the common chord.