If two straight lines intersect each other, then prove that the ray opposite the bisector of one

Let $A B$ and $C D$ be the two lines intersecting at a point $O$ and let ray $O E$ bisect $\angle A O C$. Now, draw a ray $O F$ in the opposite direction of $O E$, such that $E O F$ is a straight line.

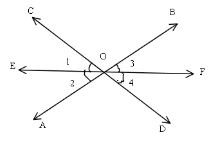
Let $\angle C O E=1, \angle A O E=2, \angle B O F=3$ and $\angle D O F=4$.

We know that vertically-opposite angles are equal.

$\therefore \angle 1=\angle 4$ and $\angle 2=\angle 3$

But, $\angle 1=\angle 2 \quad[$ Since $O E$ bisects $\angle A O C]$

$\therefore \angle 4=\angle 3$

Hence, the ray opposite the bisector of one of the angles so formed bisects the vertically-opposite angle.