Question:
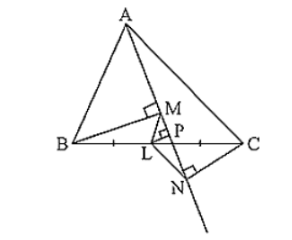
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid-point of BC, prove that ML = NL.
Solution:
Given that,
In ΔBLM and ΔCLN
∠BML = ∠CNL = 90°
BL = CL [L is the mid-point of BC]
∠MLB = ∠NLC [Vertically opposite angle]
∴ ΔBLM = ΔCLN
∴ LM = LN [corresponding parts of congruent triangles]
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
