In a ΔABC, it is given that AB = AC and the bisectors of B and C intersect at O.

Given that in ΔABC,

AB = AC and the bisector of ∠B and ∠C intersect at O. If M is a point on BO produced

We have to prove ∠MOC = ∠ABC

Since,

AB = AC

ABC is isosceles

∠B = ∠C (or)

∠ABC = ∠ACB

Now,

BO and CO are bisectors of ∠ ABC and ∠ACB respectively

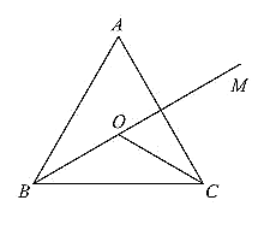
$\Rightarrow \mathrm{ABO}=\angle \mathrm{OBC}=\angle \mathrm{ACO}=\angle \mathrm{OCB}=\frac{1}{2} \angle \mathrm{ABC}=\frac{1}{2} \angle \mathrm{ACB} \ldots$ (i)

We have, in Δ OBC

∠OBC + ∠OCB + ∠BOC = 180°  ... (ii)

And also

∠BOC + ∠COM = 180° ... (iii) [Straight angle]

Equating (ii) and (iii)

∠OBC + ∠OCB + ∠BOC = ∠BOC + ∠MOC

∠OBC + ∠OCB = ∠MOC [From (i)]

2∠OBC = ∠MOC [From (i)]

$2\left(\frac{1}{2} \angle \mathrm{ABC}\right)=\angle \mathrm{MOC}[$ From $(\mathrm{i})]$

∠ABC = ∠MOC

Therefore, ∠MOC = ∠ABC