In a class test, the sum of the marks obtained by P in Mathematics and science is 28.

Solution:

Let marks obtained by $P$ in mathematics be $x$, then in science $=(28-x)$

It is given that,

$(x+3) \times(28-x-4)=180$

$(x+3) \times(24-x)=180$

$24 x-x^{2}+72-3 x=180$

$-x^{2}+21 x+72-180=0$

$-\left(x^{2}-21 x+108\right)=0$

$x^{2}-21 x+108=0$

$x^{2}-12 x-9 x+108=0$

$x(x-12)-9(x-12)=0$

$(x-12)(x-9)=0$

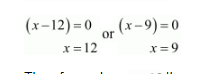
Therefore, when $x=12$ then

$(28-x)=(28-12)$

$=16$

Hence, marks in mathematics $x=12$ and marks in science $=16$.

Or, when $x=9$ then

$(28-x)=(28-9)$

$=19$

Hence, marks in mathematics $x=9$ and marks in science $=19$.