Question:
In a right $\triangle A B C$ right-angled at $C$, if $D$ is the mid-point of $B C$, prove that $B C^{2}=4\left(A D^{2}-A C^{2}\right)$.
Solution:
It is given that ∆ABC is a right-angled at C and D is the mid-point of BC.
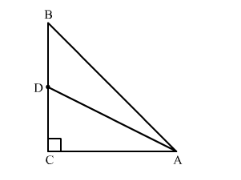
In the right angled triangle ADC, we will use Pythagoras theorem,
$A D^{2}=D C^{2}+A C^{2}$
Since $D$ is the midpoint of $B C$, we have
$D C=\frac{B C}{2}$
Substituting $D C=\frac{B C}{2}$ in equation (1), we get
$A D^{2}=\left(\frac{B C}{2}\right)^{2}+A C^{2}$
$A D^{2}=\frac{B C^{2}}{4}+A C^{2}$
$4 A D^{2}=B C^{2}+4 A C^{2}$
$B C^{2}=4 A D^{2}-4 A C^{2}$
$B C^{2}=4\left(A D^{2}-A C^{2}\right)$