In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then

Solution:

Disclaimer: There is mistake in the problem. The question should be "In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and BC respectively, then"

Given: In the right ΔABC, right angled at B. P and Q are points on the sides AB and BC respectively.

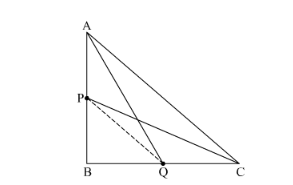
Applying Pythagoras theorem,

In ΔAQB,

$\mathrm{AQ} 2=\mathrm{AB} 2+\mathrm{BQ} 2$....(1)

In ΔPBC

$\mathrm{CP}^{2}=\mathrm{PB}^{2}+\mathrm{BC}^{2}$.....(2)

Adding (1) and (2), we get

AQ2+CP2=AB2+BQ2+PB2+BC2    .....(3)

In ΔABC,

$\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}$....(4)

In ΔPBQ,

PQ2=PB2+BQ2        .....(5)

From (3), (4) and (5), we get

AQ2+CP2=AC2+PQ2

We got the result as (c)