In ∆ABC, AD and BE are altitude. Prove that
In $\triangle \mathrm{ABC}, \mathrm{AD}$ and $\mathrm{BE}$ are altitude. Prove that $\frac{\operatorname{ar}(\Delta \mathrm{DEC})}{\operatorname{ar}(\Delta \mathrm{ABC})}=\frac{\mathrm{DC}^{2}}{\mathrm{AC}^{2}}$.
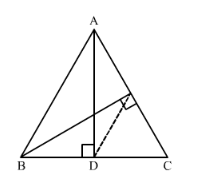
Given: ΔABC in which AD and BE are altitudes on sides BC and AC respectively.
Since ∠ADB = ∠AEB = 90°, there must be a circle passing through point D and E having AB as diameter.
We also know that, angle in a semi-circle is a right angle.
Now, join DE.
So, ABDE is a cyclic quadrilateral with AB being the diameter of the circle.
∠A + ∠BDE = 180° [Opposite angles in a cyclic quadrilateral are supplementary]
⇒ ∠A + (∠BDA + ∠ADE) = 180°
⇒ ∠BDA + ∠ADE = 180° − ∠A ..... (1)
Again,
∠BDA + ∠ADC = 180° [Linear pair]
⇒ ∠BDA + ∠ADE + ∠EDC = 180°
⇒ ∠BDA + ∠ADE = 180° − ∠EDC ..... (2)
Equating (1) and (2), we get
180° − ∠A = 180° − ∠EDC
⇒ ∠A = ∠EDC
Similarly, ∠B = ∠CED
Now, in ΔABC and ΔDEC, we have
∠A = ∠EDC
∠B = ∠CED
∠C = ∠C
∴ ΔABC ∼ ΔDEC
$\Rightarrow \frac{\text { Area of } \triangle \mathrm{DEC}}{\text { Area of } \triangle \mathrm{ABC}}=\left(\frac{\mathrm{DC}}{\mathrm{AC}}\right)^{2}$