Question:
In $\triangle A B C$, given that $A B=A C$ and $B D \perp A C$. Prove that $B C^{2}=2 A C . C D$
Solution:
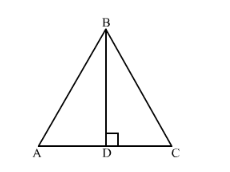
Since $\triangle A D B$ is right triangle right angled at $D$
$A B^{2}=A D^{2}+B D^{2}$
Substitute $A B=A C$
$A C^{2}=A D^{2}+B D^{2}$
$A C^{2}=(A C-D C)^{2}+B D^{2}$
$A C^{2}=A C^{2}+D C^{2}-2 A C \cdot D C+B D^{2}$
$2 A C \cdot D C=A C^{2}-A C^{2}+D C^{2}+B D^{2}$
$2 A C \cdot D C=D C^{2}+B D^{2}$
Now, in $\triangle B D C$, we have
$C D^{2}+B D^{2}=B C^{2}$
Therefore, $2 A C \cdot D C=D C^{2}+B D^{2}$
$2 A C . D C=B C^{2}$
Hence proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
